Admittance.H File Reference

Declaration of functions and classes for constructing the bus admittance matrix ($$ Y_{bus} $$) in power system analysis. More...

#include <Eigen/Dense>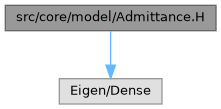

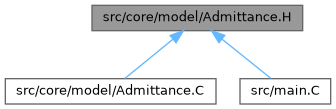
Include dependency graph for Admittance.H:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
Eigen::MatrixXcd	computeAdmittanceMatrix (const BusData &busData, const BranchData &branchData)
	Computes the complex bus admittance matrix ($$ Y_{bus} $$).

Detailed Description

Declaration of functions and classes for constructing the bus admittance matrix ($$ Y_{bus} $$) in power system analysis.

This header provides the interface for computing the admittance matrix using bus and branch data. The admittance matrix $$ Y_{bus} $$ is a fundamental element in load flow studies, relating bus currents $$ I $$ and bus voltages $$ V $$ via the equation:

$$ I = Y_{bus} V $$

where:

• $$ I $$ is the vector of injected currents,
• $$ Y_{bus} $$ is the complex bus admittance matrix,
• $$ V $$ is the vector of bus voltages.

Definition in file Admittance.H.

Function Documentation

computeAdmittanceMatrix()

Eigen::MatrixXcd computeAdmittanceMatrix	(	const BusData &	busData,
		const BranchData &	branchData
	)

Computes the complex bus admittance matrix ($$ Y_{bus} $$).

This function generates the bus admittance matrix, which is essential in solving power flow equations in electrical networks. The admittance matrix is computed using the provided bus and branch data.

Parameters

busData	Data representing the buses in the network.
branchData	Data representing the branches (lines/transformers) in the network.

Returns

Eigen::MatrixXcd The computed $$ Y_{bus} $$ matrix as a complex matrix.

Definition at line 32 of file Admittance.C.

                                                                                             {
    int nLine = branchData.From.size();
    int N = std::max(branchData.From.maxCoeff(), branchData.To.maxCoeff());  // 1-based bus indexing
 
    Eigen::MatrixXcd Ybus = Eigen::MatrixXcd::Zero(N, N);  // Size N x N, 0-based indexing internally
 
    for (int k = 0; k < nLine; ++k) {
        int from = branchData.From(k) - 1;  // Convert to 0-based
        int to   = branchData.To(k) - 1;    // Convert to 0-based
 
        std::complex<double> Z(branchData.R(k), branchData.X(k));
        std::complex<double> Y = 1.0 / Z;
 
        std::complex<double> B(0.0, 0.5 * branchData.B(k));
 
        double a = branchData.tapRatio(k);
        if (a == 0.0) {
            a = 1.0;
        }
 
        // Off-diagonal
        Ybus(from, to) -= Y / a;
        Ybus(to, from) = Ybus(from, to);  // Symmetric
 
        // Diagonal
        Ybus(from, from) += Y / (a * a) + B;
        Ybus(to, to)     += Y + B;
    }
 
    // Add shunt admittances
    int nBuses = busData.ID.size();  // Should match Gs and Bs size
 
    for (int n = 0; n < nBuses; ++n) {
        int busIndex = busData.ID(n) - 1;  // Convert to 0-based
 
        if (busIndex < 0 || busIndex >= Ybus.rows()) {
            LOG_ERROR("Warning: Bus ID {} out of bounds in Ybus", busIndex + 1);
            continue;
        }
 
        std::complex<double> Y_shunt(busData.Gs(n), busData.Bs(n));
        Ybus(busIndex, busIndex) += Y_shunt;
    }
 
    return Ybus;
}

References BranchData::B, BusData::Bs, BranchData::From, BusData::Gs, BusData::ID, LOG_ERROR, BranchData::R, BranchData::tapRatio, BranchData::To, and BranchData::X.

Here is the caller graph for this function: